Go to: Response form Real world example Example Introduction Page Morphological Institute Canada Date ¦ Translator Uebersetzung
Systematic, Morphological Problem Solving

Published by the Morphological Institute Canada Solving the 9 Points Problem systematically the morphological way

The 9 points problem is a traditional example. It is very well suited to show the difference in arbitrary thinking based on spices like luck, guts, fuzzy ways, and a truly systematic approach which will produce the result with absolute certainty - without any spices. We shall first run though the example and thereby magnify the methodically precise steps. An example from an industrial environment will be shown where big cost savings were made as a result of just one series of steps involving the particular method demonstrated here. The usual innovation team uses a complete system of interactive methods to break though barriers and produce fail-safe results.
Problem statement Goal / Objective	Given are 9 points arranged in a pattern as shown. Find the path which will connect all dots while drawing every line only once. A maximum of 4 straight lines are permitted. It must be possible to draw them without lifting the pen.
	As we look at the problem, it is useful to add information which will help to remember our thinking steps. This will enable to trace back to a definite point when necessary. For this reason, all points are marked, using characters A - I. The complete process would at this stage include a clarification process: What we have actually got, and the characteristics of the system as far as these touch the problem. Here on this demonstration page, this details will be left out. Some are integrated in the steps described below, though not all are mentioned specifically. We need to keep the page short. At the beginning of the process it is permitted to have a few intuitional trials, the examples could look like those on the next row.
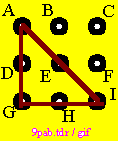
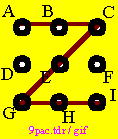
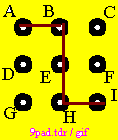
As we can see, none of these example will enable use to meet the goal / objective. However, in our systematic approach, we can use any of these trial examples as a starting situation. Even the case with the 2 short lines will work. Here we shall use the example were a triangle has been drawn.
	The first line of this triangle leads, say, from point G to point A. This is a characteristic, a form, shape. In General Morphology, this is also called a parameter. Morphology is about forms, shapes, interactions, etc. We are going to change the characteristic of this first line. We will keep the starting point G. Systematic method: NEGATION and RECONSTRUCTION. STEP 1: NEGATION of end point of line 1. The characteristic of the line becomes: Running upwards, starting at G, ending NOT at A. If the line must not end at A, where else could it end? It could end at point D ! In our trial examples we had such a case, it didn't lead to anything useful. We can also say that any line should try to touch as many points as possible. NEGATION and RECONSTRUCTION: So the line must not end in A, and should not end in D, where else? There is an infinite number of "points" where the first line could end (end points), once it crosses point A!
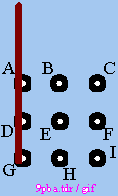	We have reconstructed the line. Its FUNCTION has not changed, it still moves through the points G-D-A. It has still the same value. The next RECONSTRUCTION step requires to meet so far untouched points in the pattern. Several posiblilities exist if we return the next line at an angle, starting anywhere on the extended first line. The line can hit single points H, E, C, and can hit two points B-I, B-F. We need as many points as possible, from the two directions, B-F looks more promising (INTUITION). There is also the likelyhood that a symmetrical construction will be of advantage (INTUITION). We select the next RECONSTRUCTION step (RATIONAL): Draw a line through B and F, extend it (RATIONAL) to meet the line through G-A.
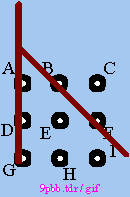	For symmetrical reasons (INTUITION), the line B-F will be extended the same way on both ends. The next line's location becomes rather obvious (RATIONAL).
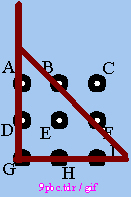	RECONSTRUCTION Line 3, analogue to line 1. There is just one line missing, to connect points E-C with the rest.
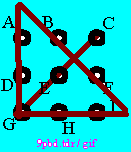	Line 4 added (RATIONAL). RECONSTRUCTION completed. Objectives and goals met. No functions lost.
Conclusion	The result was arrived at with absolute certainty, with unavoidable success. Though intuition was used, its production was guided rationally, and its results checked rationally.
Reevaluating goals	In real world applications, the process tends to provide insight which should be considered by those who set the objectives and goals. It may be necessary and a welcome fail-save procedure to reevaluate the problem statement for completeness. A rerun of of the NEGATION & RECONSTRUCTION process may be appropriate in complex cases.

To send your welcome comments directly to the author, please enter the following data: